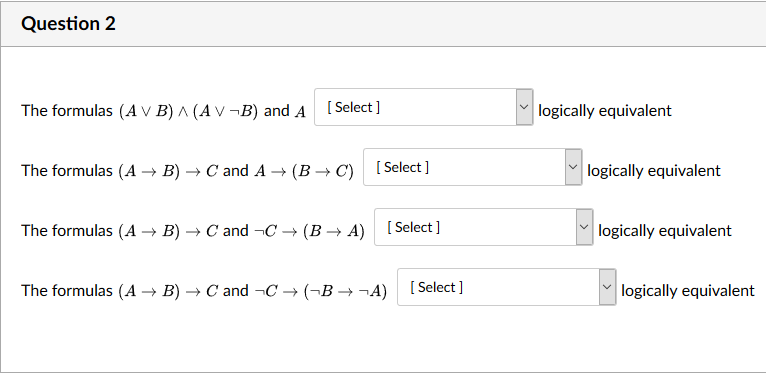
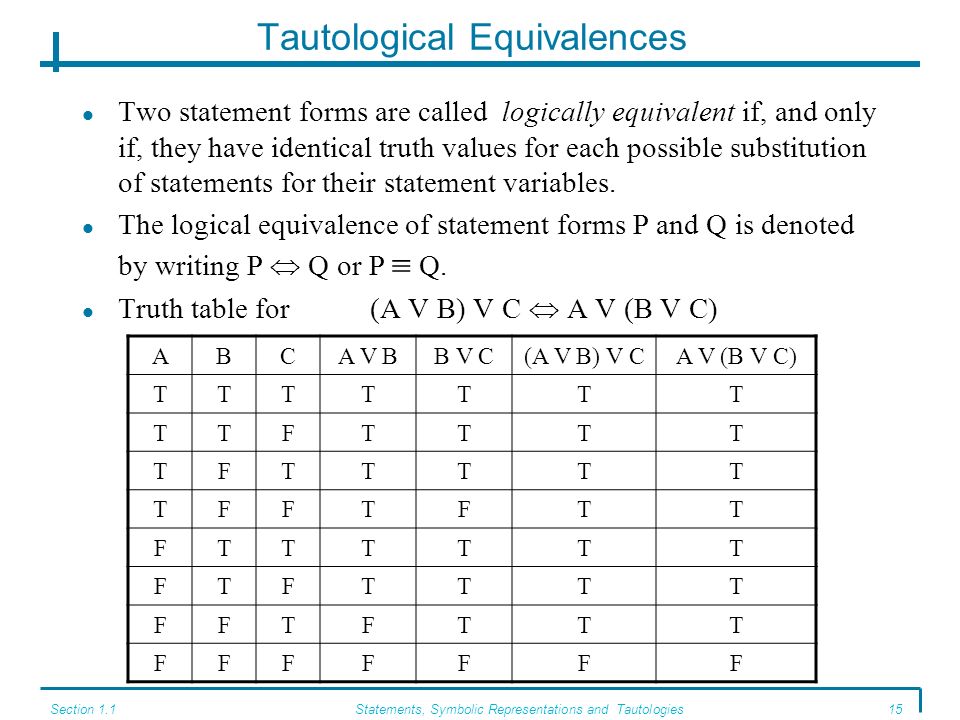
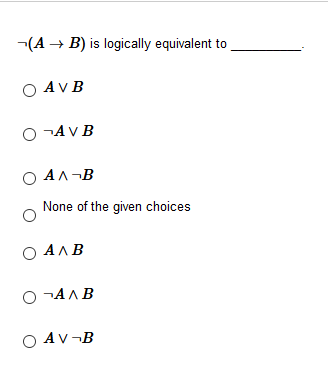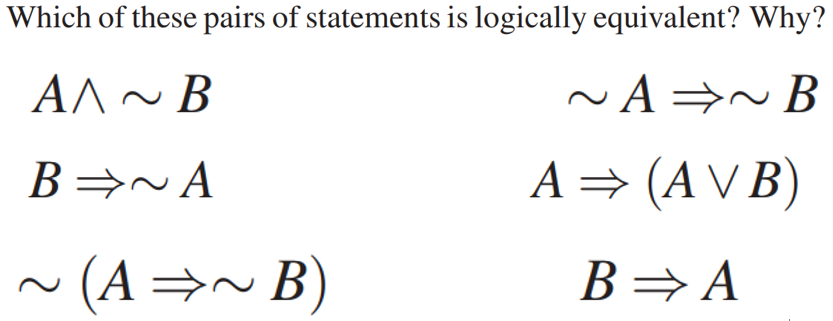A V B Is Logically Equivalent To

The two statements in this activity are logically equivalent.

A v b is logically equivalent to. Either by not having pudding or by eating your meat. A sentence of sentence logic is a logical truth just in case it is true in all possible cases that is just in case it is true for all assignments of truth values to sentence letters. So a only if b means you can have your pudding only if you eat your meat. Mathematicians normally use a two valued logic.

Assume that the equivalence a b v ë b and b c hold. Logically equivalent to p q. In logic and mathematics statements and are said to be logically equivalent if they are provable from each other under a set of axioms or have the same truth value in every model. A you can have your pudding b you eat your meat.

The following table lists many common symbols together with their name pronunciation and the related field of mathematics. Let s make it less abstract. That sounds like a mouthful but what it means is that not a and b is logically equivalent to not a or not b. In logic a set of symbols is commonly used to express logical representation.

Then truth value of the formula a b a c v d is always what can we correctly say about proposition p1 p1. I prefer to use the same expression logical truth for. Additionally the third column contains an informal definition the fourth column gives a short example the fifth and sixth give the unicode location and name for use in html documents. The law of trarrcitivity of logical equivaltnce tle.

Truth tables tautologies and logical equivalences. P v ë q q r v r v p. Repeated use of this law allows us to conclude that the first sentence in our list is logically equivalent to the last. If x is odd and y is odd then x cdot y is odd.

Such a sentence is called a logical truth. The negation of a conjunction logical and of 2 statements is logically equivalent to the disjunction logical or of each statement s negation. How can you avoid having pudding but not eating meat. Many authors use the word tautology for a logical truth of sentence logic.

Every statement is either true or false this is called the law of the excluded middle. B use the result from part 13a to explain why the given statement is logically equivalent to the following statement. For any sentences x y and z if x is logically equivalent to y and y is logically equivalent to z then x is logically equivalent to z. A statement in sentential logic is built from simple statements using the logical connectives and the truth or falsity of a statement built with these connective depends on the truth or falsity of.

Why is a only if b equivalent to not a or b. Logically equivalent symbolic definition a b iff v a v b for all v. Var t f directly from the definition we have that a b if and only if a b remember that is not a logical connective it is just a metalanguage symbol for saying a b are logically equivalent.